![]()
これは実は対数表示が役に立ちます.
もちろん,きちんと解析的は解けません.
しかし,指数関数の和の場合には,
早い反応
遅い反応
があることは前に説明しました.
つまり,
早い反応は早い時間域に影響し,
遅い反応は遅い時間域に影響する
のです.
ですから,プロットの早い時間域と遅い時間域では支配している指数関数が違い,ある程度は棲み分けが成り立つのです.
つまり,対数表示をすると,
二つの直線の折れ線
となるのです.
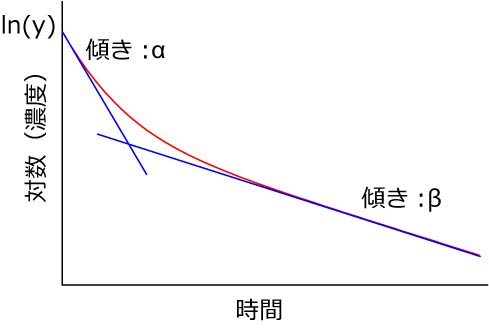
もちろん,厳密には折れ線にはならず,スムーズにつながっているのですが,その厳密な解は我々には必要ありません.
それぞれの直線の傾きを見積もることによりそれぞれの時定数を見積もることができます.
もちろん,これは二つの反応の時定数がかなり違う場合であって,ほとんど同じの場合にはとても二つの直線で表すことは難しいですね.